I collaborated with artist Allison Yeh to develop Shiny Shores, which ended up ranking 16th out of 1484 entries in Brackey’s Game Jam 2024.2. You play as a little child collecting shells and other shiny trinkets in between waves.

Hands down the most challenging part of the jam is handling the visual and mechanic of the waves.

Initially our idea was that they would come in, leave behind shiny shells, and the player needs to stay at the dock at the bottom of the screen to be safe. Somewhere along the line, we introduced rock obstacles that would block the player’s part, which is where the fun of the game truly shines.

Prototype

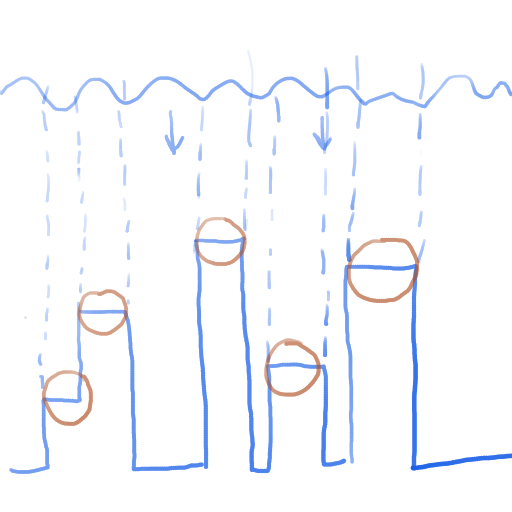My first order of business was generating the wave mesh. One approach is splitting the waves into slices that hit a particular rock. This is what I went with for the prototype.

Using a line-sweep algorithm, we can construct these slices in $O(n \log{n})$, $n$ being the number of rocks. This only needs to be recomputed when a rock emerges or sink.

List<KeyValuePair<bool, Vector2>> points = new List<KeyValuePair<bool,Vector2>>();
SortedDictionary<float, int> sweepLine = new SortedDictionary<float, int>();
List<Vector2> obstacleSliceBoundaries = new List<Vector2>();

foreach (Obstacle obstacle in obstacles) {
    SphereCollider sphereCollider = obstacle?.GetComponent<SphereCollider>();
    if (!sphereCollider) continue;
    Vector3 obstaclePosition = obstacle.transform.position;

    float crossSectionRadius = sphereCollider.radius;
    if (crossSectionRadius == 0.0) continue;

    points.Add(new KeyValuePair<bool, Vector2>(
        true, 
        new Vector2(obstaclePosition.x - crossSectionRadius, obstaclePosition.z))
    );
    points.Add(new KeyValuePair<bool, Vector2>(
        false, 
        new Vector2(obstaclePosition.x + crossSectionRadius, obstaclePosition.z))
    );
}

points.Sort((a,b) => {
    if (a.Value.x != b.Value.x) return a.Value.x.CompareTo(b.Value.x);
    if (a.Key != b.Key) return a.Key.CompareTo(b.Key);
    return 0;
});

for (int i = 0; i < points.Count; ) {
    float xPosition = points[i].Value.x;
    while (i < points.Count && xPosition == points[i].Value.x) {
        float zPosition = points[i].Value.y;

        if (sweepLine.ContainsKey(zPosition))
            sweepLine[zPosition] += (points[i].Key ? 1 : -1);
        else
            sweepLine.Add(zPosition, 1);

        if (sweepLine[zPosition] == 0) 
            sweepLine.Remove(zPosition);
        i++;
    }

    if (sweepLine.Count == 0) 
        obstacleSliceBoundaries.Add(new Vector2(xPosition, Mathf.NegativeInfinity));
    else {
        var firstItem = sweepLine.GetEnumerator();
        firstItem.MoveNext();

        float lowestKey = firstItem.Current.Key;
        obstacleSliceBoundaries.Add(new Vector2(xPosition, lowestKey));
    }
}

Iteration

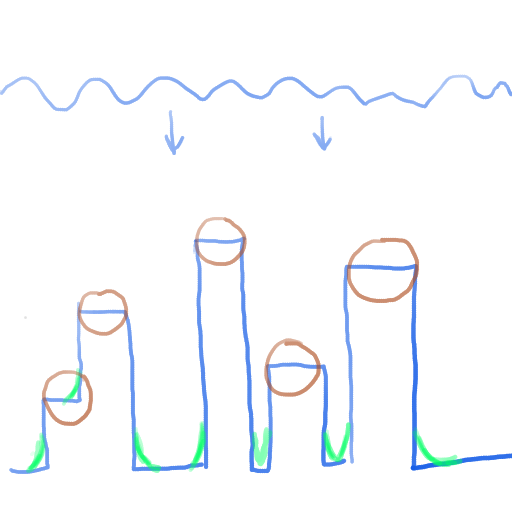With the prototype approach, however, we end up with quite rectangular waves. Every slice is a quad afterall. In Shiny Shores we wanted the waves to look more organic and that means absolutely no sharp edges. Ideally, it would look like the image to the right.

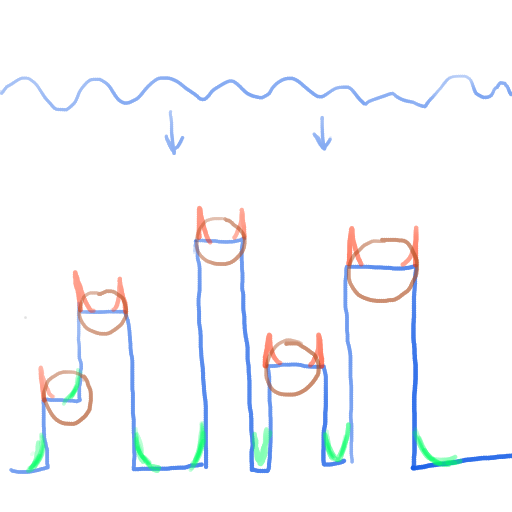We can add smoothed out borders to the wave slices in shader. However, we would run into unintended borders. Of course, one workaround is to determine if a left or right border is added to a slice by looking at whether neighboring slices, but this approach is inellegant.

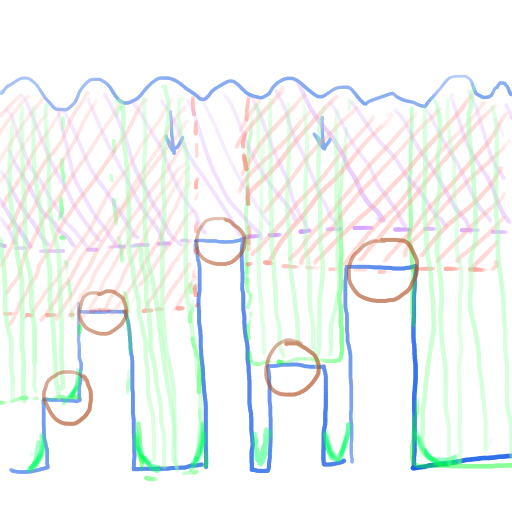After some thinking, it dawned on me that the wave slices need not be disjoint. They can intersect! As long as the UVs are lined up correctly, z fighting will not matter since there’s visually no artifact.

The code for this is quite similar to a quicksort. First find the shortest wave slice, then make a giant wave covering the whole arena up to the length of that slice, then recurse on the left and right.